例题集2
向量场保守性与曲线积分两题的解答
3.4.46 练习题(Übung)#
计算积分 $\int_K \mathbf{f} \cdot d\mathbf{s}$ 的值,其中向量场
$$ \mathbf{f} : \mathbb{R}^2 \to \mathbb{R}^2, \quad \mathbf{f}(x,y) = \begin{pmatrix} 2xy + y^2 \\ 2xy + x^2 \end{pmatrix}. $$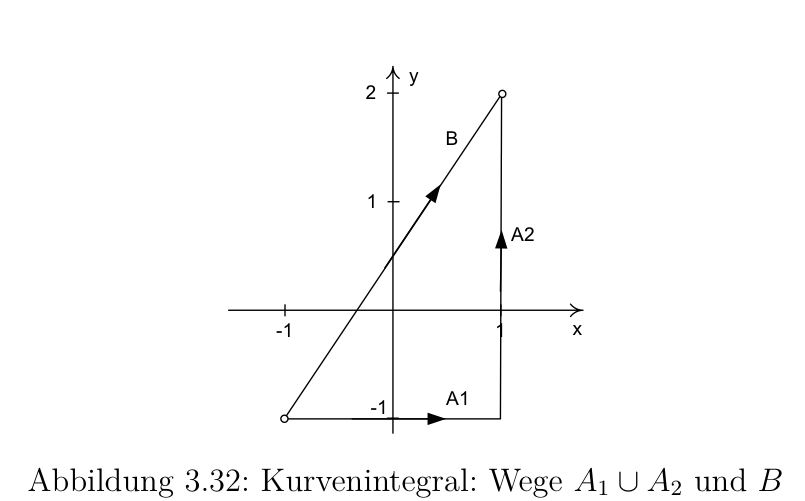
分别针对以下路径:
(i) 由线段 A1 与 A2 组成的曲线(参见图 3.32);
(ii) 由线段 B 组成的曲线;
(iii) 通过求向量场 $\mathbf{f}$ 的势函数 $\varphi$(并任取一条从 $(-1,-1)$ 到 $(1,2)$ 的曲线)。
解:判断并求势函数,曲线积分与路径无关。
- 保守性:$\frac{\partial f_1}{\partial y} = 2x + 2y,\ \frac{\partial f_2}{\partial x} = 2x + 2y$,相等 ⇒ 场保守。
- 势函数: $$ \varphi = \int (2xy + y^2)\dx = x^2 y + x y^2 + C(y) $$ 由 $\frac{\partial \varphi}{\partial y} = x^2 + 2xy + C’(y) = f_2$ 得 $C’(y)=0$,故 $$ \boxed{\varphi(x,y)=x^2 y + x y^2 + \text{const}} $$
- 端点取 $P=(-1,-1)$,$Q=(1,2)$(三条路径端点相同): $$ \varphi(Q)=1^2\cdot2 + 1\cdot4 = 6,\qquad \varphi(P)=(-1)^2(-1) + (-1)\cdot1 = -2 $$ $$ \int_K \mathbf{f}\cdot d\mathbf{s} = \varphi(Q)-\varphi(P) = 6 - (-2) = \boxed{8} $$ 因为是保守场,A1+A2、B 或任意曲线结果都相同,均为 8。
3.4.47 练习题(Übung)#
计算积分 $\int_C \mathbf{f} \cdot d\mathbf{s}$ 的值,其中积分路径 $C$ 从点 $P_1 = (1,0,1)$ 到点 $P_2 = (2,3,2)$,向量场为
$$ \mathbf{f} : \mathbb{R}^3 \to \mathbb{R}^3, \quad \mathbf{f}(x,y,z) = \begin{pmatrix} 3x^2y + 1 \\ x^3 + 2yz^2 \\ 2y^2z + 3z^2 \end{pmatrix}. $$解:同样先判保守性并求势函数。
- 保守性检查: $$ \frac{\partial f_1}{\partial y} = 3x^2 = \frac{\partial f_2}{\partial x},\quad \frac{\partial f_1}{\partial z} = 0 = \frac{\partial f_3}{\partial x},\quad \frac{\partial f_2}{\partial z} = 4yz = \frac{\partial f_3}{\partial y} $$ 均相等 ⇒ 场保守。
- 势函数:
$$
\varphi = \int (3x^2 y + 1),dx = y x^3 + x + C(y,z)
$$
用 $f_2$:$\frac{\partial \varphi}{\partial y} = x^3 + C_y = x^3 + 2yz^2 \Rightarrow C_y = 2yz^2$
$$
C(y,z) = y^2 z^2 + D(z)
$$
再用 $f_3$:$\frac{\partial \varphi}{\partial z} = 2y^2 z + D’(z) = 2y^2 z + 3z^2 \Rightarrow D’(z)=3z^2$,
故 $D(z)=z^3 + \text{const}$,于是 $$ \boxed{\varphi(x,y,z)=y x^3 + x + y^2 z^2 + z^3 + \text{const}} $$ - 端点代入: $$ \varphi(P_1) = 0\cdot1^3 + 1 + 0 + 1 = 2;\qquad \varphi(P_2) = 3\cdot 2^3 + 2 + 3^2\cdot 2^2 + 2^3 = 24 + 2 + 36 + 8 = 70 $$ $$ \int_C \mathbf{f}\cdot d\mathbf{s} = \varphi(P_2) - \varphi(P_1) = \boxed{68} $$ 路径任意(只要端点相同)结果都为 68。